Practical Conversion of dB and Power
- The dB value plus 3 and the power value will double; The dB value is reduced by 3 and the power value is halved
- The dB value plus 10 and the power value is multiplied by 10; The dB value minus 10 and the power value divided by 10
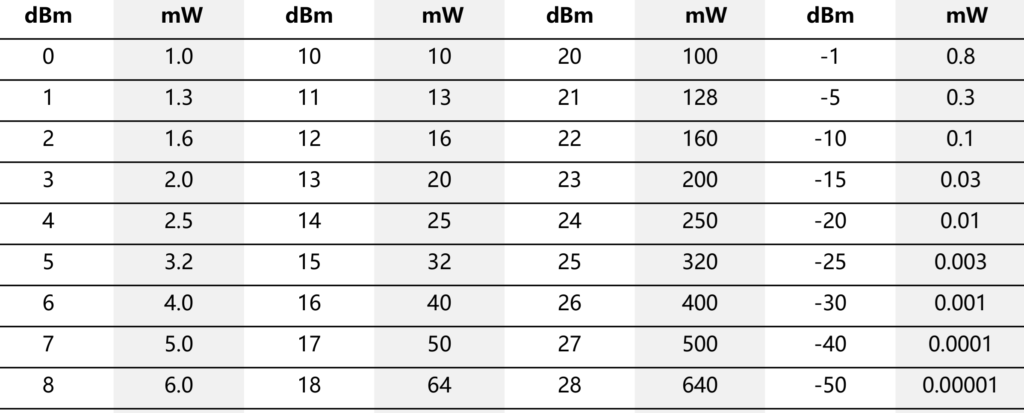
Note: The above formula is an example of power unit conversion. To verify the formula, please refer to the “dbm and mW conversion comparison table”. The dB formula can also be applied to other physical units.
dnm to mW conversion table
dB (decibel) is a Dimensionless units, used to indicate the relative value of a physical quantity, usually used to describe signal strength, power, voltage, etc.
Dimensionless units refer to the fact that in the representation of physical quantities, no specific units are involved, but rather purely numerical comparisons or relative values. The physical quantities expressed by these units are independent of the choice of any particular units and express only relative size or comparison.
In some cases, the use of dimensionless units can simplify the description of physical quantities and make comparisons more intuitive and convenient. They are often used to describe relative quantities, such as ratios, proportions, or relative growth.
dBm is a power-specific decibel unit that represents the logarithmic ratio of power relative to 1 milliwatt. The power is described by the logarithmic ratio relative to a reference power of 1 mW.
Table of Contents
ToggleCalculation between dBm and dB
dBm indicates the relative value of power relative to 1mW, and dB indicates gain/attenuation, or the relative strength of two signals.
The gain/attenuation of power values in dBm can be calculated using addition and subtraction.
For example, if the power value is 5dBm and the gain is 10dB, the power after gain is 15dBm. Another example: if a power value is 21dBm and is attenuated by 17dB, the power value after attenuation is 4dBm.
How to convert W/mW to dBm
Conversion formula
dBm = 10*lg(A/B)
Note: A is the power to be converted (the unit can be W or mW and other power units), which needs to be converted into a value in mW; B is 1mW.
Common units of power and conversion relationships
The unit of power is watt (W), and the corresponding units include mW, μW, and nW.
The conversion relationship between them is:
1W=1000mW=1000000μW=1000000000nW
For example: To convert 1W to a value in dBm, first convert 1W to a value in mW, which is 1000mW; Then substitute into the formula. 10*lg(1000mW/1mW) = 10*lg1000 = 10*3 = 30dBm
- Does dbm represent absolute intensity or relative intensity?
The dBm unit is obtained by converting the power (absolute value) to a decibel value and then referring to a reference power (usually 1 milliwatt). It represents the power level of the signal relative to 1 milliwatt, rather than the absolute power value. When we compare the dBm values of two signals, we are actually comparing their power levels relative to the same reference point.
- Why use the unit dBm?
dBm provides a relatively intuitive way to express the power level of a signal. Compared to directly using watts (W) as a unit, dBm can express the relative strength of a signal more conveniently and is easier to compare, analyze, measure, and debug.
dBm uses a logarithmic scale, which can better express a wide range of power, from extremely weak signals to very powerful signals, all of which can be represented in a smaller number range.
dBm provides a standardized way to describe signal strength without having to consider the absolute power values of different signals. It is convenient to measure and compare signal strength.
dBm, one of the most commonly used power units in the field of wireless communications, is widely used in engineering practice. Using dBm units can make communication between engineers more concise and clear.
- The decibel value is based on logarithms, and this concept requires a certain mathematical foundation. Doesn’t this increase the threshold of understanding?
Yes, the concept of decibel values is based on logarithms, which does require a certain amount of mathematical foundation to understand.
For the average user or non-specialist, it may take some time to understand the concept of this logarithmic scale. But in engineering and science, it has become the standard unit because it provides a better way to handle a wide range of data and is very useful in real-world applications. So, while it may take some time for some people to understand, once you grasp the concept, you can process and analyze relevant data more effectively.
- Why is 1mW often used as the reference level?
The main purpose is to balance the wide range of power and commonality.
Suitable power range: 1mW as a reference power covers the common power levels in many communication systems, including both weak signals and relatively strong signals.
Readability and convenience: Using 1mW as the reference power, the values in dBm units will usually be in a smaller range, more consistent with common signal power levels, and easier to understand and compare.
Engineering practice and standardization: 1mW has been widely accepted and applied as a reference power in engineering practice and has become a universal standard. This standardization makes it more convenient and uniform for engineers and technicians to design, debug and compare electronic equipment, reducing misunderstandings or confusion caused by different power units. For example, 0.00001mW converted to dBm is -50dBm, while 1000000mW converted to dBm is 60dBm. These values within the range of ±100dBm are easier to handle and compare.
In addition, the use of dBm units also makes relative changes in power easier to identify. Taking 1mW as the reference power, every increase or decrease of 3dBm will double or halve the power. This logarithmic relationship makes the dBm unit very suitable for describing relative changes in power, which is very helpful for engineering design and equipment debugging.
- Can other units be used as reference?
Yes, you can also use W as the reference unit, which is the origin of dBW.
Conversion formula:
dBW = 10*lg(A/B)
Note: A is the power to be converted; B is 1W. 10*lg(1W/1W)= 10*lg1 = 10*0= 0dBW
- How much power is 1dBm?
Substitute into the formula: 1dBm = 10*lg (A/1mW)
A = 10^0.1≈1.25892mW, so 1dBm corresponds to a power value of approximately 1.3mW.
The power value in dBm can be estimated with the help of some special values.
For example, when estimating the power value of 2.5dBm, 0dBm is relatively easy for us, because we know that it corresponds to 1mW, and we also know that the gain value of 3dB is approximately one times, that is to say, 3dBm is approximately 2mW. Then according to 2.5/3*2mW, we can get an estimated value of 1.67mW, and the actual value of 2.5dBm is 1.7783mW, which are relatively close. Of course, this is only used for estimation.
- Since when did the unit of dBm come into being?
The dBm unit has a long history in wireless communications and electronic engineering. Its origins can be traced back to the early 20th century. With the development of communication technology and the popularization of electronic devices, engineers needed a convenient and standardized way to describe the power level of signals. Early telecommunications engineers began using decibels (dB) to express the relative strength of a signal, and later introduced the dBm unit with 1mW as the reference power to make it easier to compare and describe signal power levels. Over time, dBm has become one of the standard power units widely used in wireless communications and electronic engineering.
Universal units often arise from practical needs, especially in science, engineering, and technology, where units need to be able to accurately describe and measure phenomena, processes, or properties of matter. For example, the dBm unit was introduced to make it easier to compare power levels in electronic devices, especially in the field of communications.
As technology develops and industry needs change, these units are formed through consensus among professionals, reviewed by standardization organizations, and formulated as international standards, and eventually become widely used. This process ensures the widespread acceptance and accuracy of the units, making them recognized standards globally or within a specific field. The formation of such consensus not only facilitates the exchange of technology and information, but also helps promote development and innovation in related fields. Therefore, the widespread use and standardization of units lay a solid foundation for scientific and technological progress and international cooperation.
